1.7 错误检测和纠正码

在本教程中，我们将学习一些常用的错误检测与纠正码。我们将探讨数字通信中的错误类型，以及像奇偶校验、CRC（循环冗余校验）、汉明码等错误检测与纠正码。

在数字系统中，模拟信号会转换为数字序列（以比特的形式）。这种比特序列被称为“数据流”。数据流中单个比特位置的改变也可能导致数据输出中出现灾难性的错误。几乎在所有电子设备中，我们都会遇到错误，因此我们使用错误检测与纠正技术来获得准确或近似的结果。

什么是错误

在数据传输过程中（从源到接收器），数据可能会受到外部噪声或其他物理缺陷的影响。在这种情况下，输入数据与接收到的输出数据不一致。这种不匹配的数据被称为“错误”。

数据错误会导致重要或安全数据的丢失。即使数据中只有一个比特的改变，也可能影响整个系统的性能。在数字系统中，数据传输通常以“比特传输”的形式进行。在这种情况下，数据错误可能会导致0和1的位置发生改变。

错误类型

在数据序列中，如果1变为0，或者0变为1，这种情况被称为“比特错误”。在数据传输过程中，从发射器到接收器通常会出现以下3种类型的错误：

• 单比特错误
• 多比特错误
• 突发错误

单比特错误
在整个数据序列中，一个比特的改变被称为“单比特错误”。在串行通信系统中，单比特错误的发生非常罕见。这种错误通常只在并行通信系统中出现，因为数据是按位逐行传输的，单行可能会受到噪声干扰。

多比特错误
如果在从发射器到接收器的数据序列中，有两个或多个比特发生改变，这种情况被称为“多比特错误”。这种错误在串行和并行数据通信网络中都可能出现。

突发错误
数据序列中一组比特的改变被称为“突发错误”。突发错误是从第一个比特改变到最后一个比特改变之间的范围计算的。

在这里，我们从第4位到第6位识别出错误。第4位和第6位之间的数字也被视为错误。这一组比特被称为“突发错误”。这些比特从发射器到接收器的变化可能会导致数据序列中出现重大错误。这种错误在串行通信中出现，并且很难解决。

错误检测码

在数字通信系统中，错误会与数据一起从一个通信系统传输到另一个通信系统。如果这些错误未被检测和纠正，数据将会丢失。为了实现有效的通信，数据必须以高精度传输。这可以通过首先检测错误，然后纠正它们来实现。

错误检测是检测从发射器传输到接收器的数据中存在的错误的过程。我们通过在数据传输过程中添加一些冗余码来检测这些错误。这些码被称为“错误检测码”。

错误检测类型

• 奇偶校验
• 循环冗余校验（CRC）
• 横向冗余校验（LRC）
• 校验和

奇偶校验

奇偶校验位是在发射器处添加到数据中的一个额外比特。在添加奇偶校验位之前，会计算数据中1的数量或0的数量。根据这一计算结果，会在实际信息/数据中添加一个额外的比特。添加奇偶校验位会导致数据字符串大小的改变。

这意味着，如果我们有一个8位的数据，那么在添加了一个奇偶校验位之后，数据二进制字符串将变成一个9位的二进制数据字符串。

奇偶校验也被称为“垂直冗余校验（VRC）”。

在错误检测中，有两种类型的奇偶校验位，分别是：

• 偶校验
• 奇校验

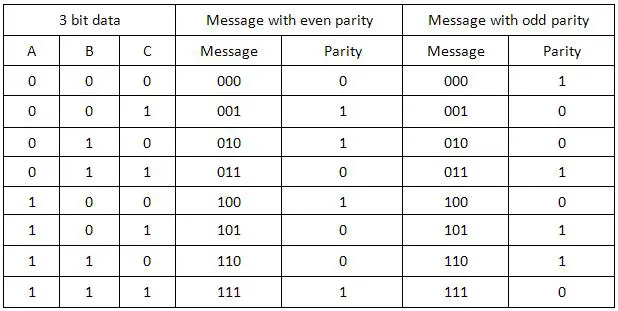
偶校验
如果数据中有偶数个1，则奇偶校验位为0。例如：数据为10000001 → 奇偶校验位为0。
如果数据中有奇数个1，则奇偶校验位为1。例如：数据为10010001 → 奇偶校验位为1。

奇校验
如果数据中有奇数个1，则奇偶校验位为0。例如：数据为10011101 → 奇偶校验位为0。
如果数据中有偶数个1，则奇偶校验位为1。例如：数据为10010101 → 奇偶校验位为1。

注意：数据比特的计数包括奇偶校验位。

在发射器处为数据添加奇偶校验位的电路被称为“奇偶校验生成器”。奇偶校验位会随数据一起传输，并在接收器处进行检查。如果发射器发送的奇偶校验位与接收器接收到的奇偶校验位不相等，则检测到错误。在接收器处检查奇偶校验的电路被称为“奇偶校验检查器”。

循环冗余校验（CRC）

循环码是一种线性$(n, k)$分组码，具有这样的特性：一个码字的任何循环移位都会得到另一个码字。其中，$k$表示发射器处消息的长度（信息比特的数量），$n$是添加校验比特后的消息总长度（实际数据和校验比特）。$n - k$是校验比特的数量。

用于循环冗余校验的码被称为CRC码（循环冗余校验码）。循环冗余校验码是缩短的循环码。这种类型的码用于错误检测和编码。它们可以通过带有反馈连接的移位寄存器轻松实现，因此被广泛用于数字通信中的错误检测。CRC码可以提供高效且高级别的保护。

CRC码生成
根据所需的比特校验数量，我们会在实际数据中添加一些零（0）。这个新的二进制数据序列会除以一个长度为$n + 1$的新字，其中$n$是要添加的校验比特的数量。这个模2除法的结果余数会被添加到被除数比特序列中，形成循环码。生成的码字可以被用于生成码的除数整除。这个码字通过发射器传输。

示例

在接收端，我们将接收到的码字用相同的除数进行除法运算，以获得实际的码字。对于无错误的数据接收，余数为0。如果余数非零，则表示接收到的码/数据序列中存在错误。错误检测的概率取决于用于构造循环码的校验比特数量$n$。对于单比特和双比特错误，检测概率为100%。

对于长度为$n - 1$的突发错误，检测概率为100%。
对于长度为$n + 1$的突发错误，检测概率降低为$1 - \frac{1}{2^{n-1}}$。
对于长度大于$n - 1$的突发错误，检测概率为$1 - \frac{1}{2^n}$。

横向冗余校验

在横向冗余校验方法中，一组比特被排列成表格格式（按行和列），我们分别计算每一列的奇偶校验位。这些奇偶校验位也会与原始数据位一起传输。

横向冗余校验是一种逐位奇偶校验计算方法，因为我们分别计算每一列的奇偶校验。

这种方法可以轻松检测突发错误和单比特错误，但无法检测在同一垂直切片中出现的两个比特错误。

校验和
校验和类似于奇偶校验位，但校验和的位数比奇偶校验位多，且结果始终被约束为零。这意味着如果校验和为零，则检测到错误。消息的校验和是某些长度的码字的算术和。这个和通过1的补码表示，并作为实际码字的扩展码存储或传输。在接收端，通过接收发射器的比特序列重新计算校验和。

校验和方法包括奇偶校验位、校验数字和横向冗余校验（LRC）。例如，如果我们需要传输并检测一个长数据序列（也称为数据字符串）的错误，我们可以将数据分割成较短的字，并将数据存储为相同宽度的字。对于每一个新输入的比特，我们将它们添加到已存储的数据中。在每个时刻，新添加的字被称为“校验和”。

在接收端，如果接收到的比特序列的校验和与发射器的校验和相同，则未发现错误。

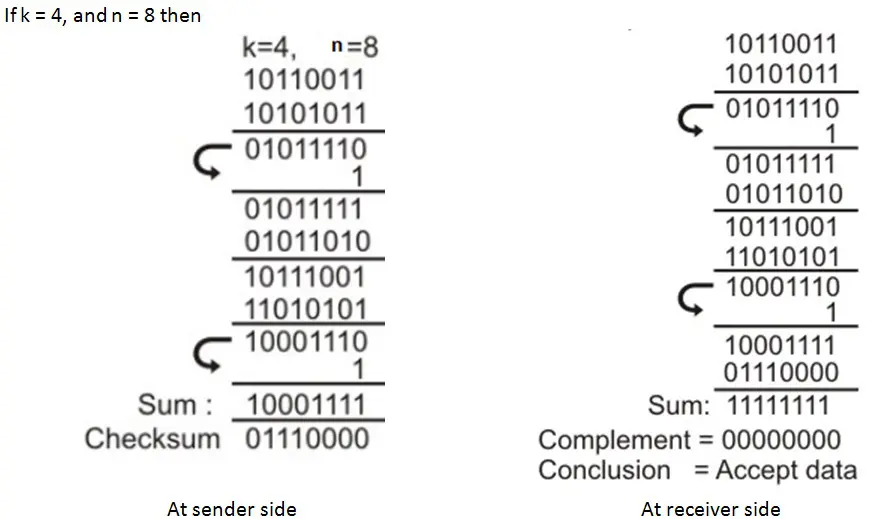
我们也可以通过添加所有数据位来找到校验和。例如，如果我们有4个字节的数据：25H、62H、3FH、52H。

那么，将所有字节相加得到118H。

丢弃进位的半字节，得到18H。

找到该半字节的2的补码，即E8H。

这就是传输的4个比特数据的校验和。

在接收端，为了检查数据是否无误接收，只需将校验和与实际数据位相加（我们会得到200H）。通过丢弃进位的半字节，我们得到00H。这意味着校验和被约束为零。因此，数据中没有错误。

一般来说，有5种类型的校验和方法，分别是：

• 整数加法校验和
• 1的补码校验和
• Fletcher校验和
• Adler校验和
• ATN校验和（AN/466）

示例

到目前为止，我们已经讨论了错误检测码。然而，仅通过检测数据中出现的错误，是无法接收完全准确无误的数据序列的。我们还需要通过消除错误来纠正数据。为此，我们使用一些其他码。

错误纠正码

用于错误检测和错误纠正的码被称为“错误纠正码”。错误纠正技术分为两种类型，分别是：

• 单比特错误纠正
• 突发错误纠正

纠正单比特错误的过程或方法被称为“单比特错误纠正”。检测并纠正数据序列中的突发错误的方法被称为“突发错误纠正”。

汉明码（或汉明距离码）是我们大多数通信网络和数字系统中使用的最佳错误纠正码。

汉明码

这种错误检测与纠正码技术是由R.W.汉明开发的。这种码不仅能识别整个数据序列中的错误比特，还能纠正它。这种码使用一定数量的奇偶校验位，这些校验位位于码字的特定位置。奇偶校验位的数量取决于信息比特的数量。汉明码利用冗余位与数据位之间的关系，这种码可以应用于任意数量的数据位。

什么是冗余位？
冗余表示“实际数据序列的比特数与传输比特数之间的差异”。这些冗余位用于通信系统中检测和纠正错误（如果有的话）。

汉明码是如何纠正错误的？
在汉明码中，冗余位被放置在某些经过计算的位置，以消除错误。两个冗余位之间的距离被称为“汉明距离”。

为了理解汉明码的工作原理以及数据错误纠正和检测机制，让我们来看以下阶段。

奇偶校验位的数量
正如我们之前学到的，要添加到数据字符串中的奇偶校验位的数量取决于要传输的数据字符串中的信息比特的数量。奇偶校验位的数量将通过使用数据比特来计算。这种关系如下所示。

$2^P \geq n + P + 1$

这里，$n$表示数据字符串中的比特数。

$P$表示奇偶校验位的数量。

例如，如果我们有一个4位的数据字符串，即$n = 4$，那么可以通过试错法找到要添加的奇偶校验位的数量。假设$P = 2$，那么

$2^P = 2^2 = 4 \quad \text{和} \quad n + P + 1 = 4 + 2 + 1 = 7$

这违反了实际表达式。

因此，我们尝试$P = 3$，那么

$2^P = 2^3 = 8 \quad \text{和} \quad n + P + 1 = 4 + 3 + 1 = 8$

因此，对于4位数据，需要3个奇偶校验位来进行单比特错误纠正。

奇偶校验位的放置位置
在计算出所需的奇偶校验位数量后，我们需要知道在信息字符串中放置它们的合适位置，以提供单比特错误纠正。

在上述考虑的例子中，我们有4个数据位和3个奇偶校验位。因此，要传输的总码字为7位（4 + 3）。我们通常从右到左表示数据序列，如下所示。

bit 7, bit 6, bit 5, bit 4, bit 3, bit 2, bit 1, bit 0

奇偶校验位必须位于2的幂次位置，即1、2、4、8和16等。因此，包含奇偶校验位后的码字如下所示

D7, D6, D5, P4, D3, P2, P1

这里P1、P2和P3是奇偶校验位。D1到D7是数据位。

构建比特位置表
在汉明码中，每个奇偶校验位都会检查并帮助在整个码字中找到错误。因此，我们必须找到奇偶校验位的值，以便为它们分配比特值。

通过计算并将奇偶校验位插入到数据位中，我们可以通过汉明码实现错误纠正。

让我们通过一个例子来清楚地理解这一点。

示例：

使用汉明码将数据1101以偶校验编码。

步骤1

计算所需的奇偶校验位数量。

假设$P = 2$，那么

$2^P = 2^2 = 4 \quad \text{和} \quad n + P + 1 = 4 + 2 + 1 = 7$

2个奇偶校验位对于4位数据是不够的。

因此，我们尝试$P = 3$，那么

$2^P = 2^3 = 8 \quad \text{和} \quad n + P + 1 = 4 + 3 + 1 = 8$

因此，3个奇偶校验位对于4位数据是足够的。

码字中的总比特数为4 + 3 = 7。

步骤2

构建比特位置表。

步骤3

确定奇偶校验位。

对于P1：第3、5和7位有三个1，因此对于偶校验，P1 = 1。

对于P2：第3、6和7位有两个1，因此对于偶校验，P2 = 0。

对于P3：第5、6和7位有两个1，因此对于偶校验，P3 = 0。

通过在各自的位置插入奇偶校验位，可以形成并传输码字。它是1100101。

注意：如果码字全为零（例如：0000000），则汉明码中没有错误。

为了用字母和数字表示二进制数据，我们使用字母数字码。

字母数字码

字母数字码本质上是用于表示字母数字数据的二进制码。由于这些码通过字符表示数据，因此字母数字码也被称为“字符码”。

这些码可以表示包括字母、数字、标点符号和数学符号在内的所有类型的数据，这些数据以计算机可接受的形式呈现。这些码被实现在键盘、显示器、打印机等输入/输出设备中。 在早期，穿孔卡片被用来表示字母数字码。

它们是：

• 莫尔斯码（MORSE code）
• 博多码（BAUDOT code）
• 霍勒瑞斯码（HOLLERITH code）
• ASCII码（ASCII code）
• 扩展二进制编码十进制交换码（EBCDI code）
• Unicode（UNICODE）

莫尔斯码

在计算机和数字电子时代的初期，莫尔斯码非常流行且被广泛使用。它是由塞缪尔·F·B·莫尔斯（Samuel F.B.Morse）于1837年发明的。这是电信中首次使用的电报码。它主要用于电报信道、无线电信道以及空中交通管制单位。

博多码

这种码是由法国工程师埃米尔·博多（Emile Baudot）于1870年发明的。它是一个5单元码，即它使用5个元素来表示一个字母。它也用于电报网络中传输罗马数字。

霍勒瑞斯码

这种码是由赫尔曼·霍勒瑞斯（Herman Hollerith）于1896年创立的公司开发的。用于根据传输信息打孔卡片的12位码被称为“霍勒瑞斯码”。

ASCII码

ASCII代表美国信息交换标准代码。它是世界上最受欢迎且广泛使用的字母数字码。该码于1967年首次开发并发布。ASCII码是一个7位码，这意味着该码使用$2^7 = 128$个字符。它包括：

• 26个小写字母（a-z）
• 26个大写字母（A-Z）
• 33个特殊字符和符号（如! @ # $等）
• 33个控制字符（如* - + /和%等）
• 10个数字（0-9）

在这个7位码中，我们有两个部分：最左边的3位和右边的4位。最左边的3位被称为“区域位（ZONE bits）”，右边的4位被称为“数值位（NUMERIC bits）”。

8位ASCII码可以表示256个字符（$2^8$）。它被称为USACC-II或ASCII-8码。

示例：
如果我们想打印名字“LONDAN”，其ASCII码为：

• L 的ASCII-7等价为 $100\ 1100$
• O 的ASCII-7等价为 $100\ 1111$
• N 的ASCII-7等价为 $100\ 1110$
• D 的ASCII-7等价为 $100\ 0100$
• A 的ASCII-7等价为 $100\ 0001$
• N 的ASCII-7等价为 $100\ 1110$

“LONDAN”在ASCII码中的输出是1 0 0 1 1 0 0 1 0 0 1 1 1 1 1 0 0 1 1 1 0 1 0 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 1 1 1 0。

UNICODE

ASCII码和EBCDIC码的缺点在于它们并不兼容所有语言，并且没有足够的字符集来表示所有类型的数据。为了克服这些缺点，开发了UNICODE。
UNICODE是所有数字编码技术的新概念。在这种编码中，我们用不同的字符来表示每一个数字。它是一种最先进且复杂的语言，能够表示任何类型的数据，因此被称为“通用码”。它是一个16位的编码，可以表示$2^{16} = 65536$个不同的字符。
UNICODE是由UNICODE联盟和国际标准化组织（ISO）共同开发的。

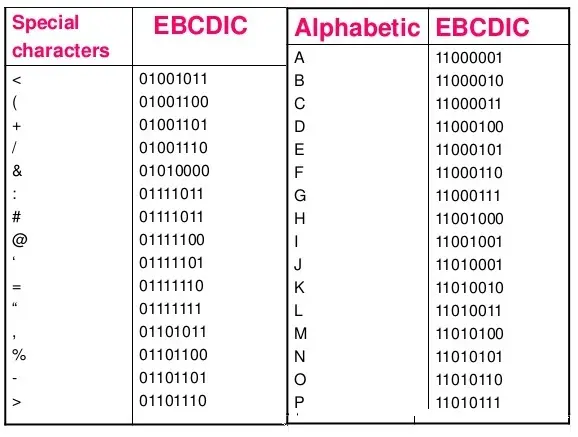
EBCDIC码

EBCDIC代表扩展二进制编码十进制交换码。这种编码是由IBM公司开发的。它是一个8位的编码，因此可以使用EBCDIC码表示$2^8 = 256$个字符。这包括所有字母和符号，例如26个小写字母（a–z）、26个大写字母（A–Z）、33个特殊字符和符号（如! @ # $等）、33个控制字符（如* – + /和%等）以及10个数字（0–9）。

在EBCDIC编码中，8位编码中的数字由8421 BCD码表示，且前面带有1111。